Laplacian matrix

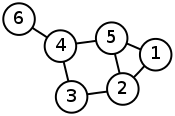
In the mathematical field of graph theory, the Laplacian matrix, sometimes called admittance matrix, Kirchhoff matrix or discrete Laplacian, is a matrix representation of a graph. The Laplacian matrix can be used to find many useful properties of a graph. Together with Kirchhoff's theorem, it can be used to calculate the number of spanning trees for a given graph. The sparsest cut of a graph can be approximated through the second smallest eigenvalue of its Laplacian by Cheeger's inequality. It can also be used to construct low dimensional embeddings, which can be useful for a variety of machine learning applications. Given a simple graph G {displaystyle G} with n {displaystyle n} vertices, its Laplacian matrix L n × n { extstyle L_{n imes n}} is defined as: where D is the degree matrix and A is the adjacency matrix of the graph. Since G { extstyle G} is a simple graph, A { extstyle A} only contains 1s or 0s and its diagonal elements are all 0s. In the case of directed graphs, either the indegree or outdegree might be used, depending on the application. The elements of L { extstyle L} are given by where deg ⁡ ( v i ) {displaystyle operatorname {deg} (v_{i})} is the degree of the vertex i {displaystyle i} . The symmetric normalized Laplacian matrix is defined as: The elements of L sym { extstyle L^{ ext{sym}}} are given by